等向性與非等向性變異
在地理統計的分析當中，會產生方向性的影響可以分成兩大部分，一為全域性的趨勢，一為半變異圖模型中非等向性的設定。全域性的趨勢可以透過一些數學的推算模式（如：多項式）來推估，並可以在進行地理統計分析時將其影響排除。
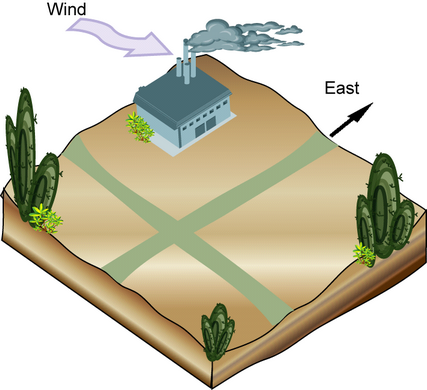
風向極有可能造成一工廠排放廢氣時對周圍區域環境的影響
在等向性與非等向性方面，地理統計利用變異圖表現空間變異的關係，而變異圖模型則是距離的函數。當空間變數之變異圖僅為距離的函數，且不因空間方向之不同而變化時，稱為等向性變異。反之，若變異因空間的方向不同而改變時，此現像稱為非等向性變異。換言之，非等向性變異之變異圖模式為「距離」與「方向」的函數，可以下列表示：
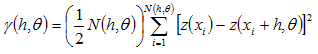
θ：沿點
與
之角度
：沿點與之角度，樣本點間距為h之組數。
若有兩區域化變數z與y，其聯合變異圖可由下式求得：
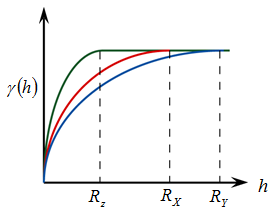
一般而言，等向性變異與非等向性變異之特性判定之步驟相同，皆是沿各方向進行套用變異圖模式，進而得到各方向之變異圖。透過變異圖可得到各方向之Sill值、影響範圍（range）與碎塊效應（Nugget Effect），最後即透過此三值來判定空間資料之等向性或非等向性。若沿各方向之變異圖模式的Sill值、Range與Nugget均相同，即可知其為等向性，反之則為非等向性。
而非等向性變異依其結構不同又可分為幾何型非等向性（Goemetric Anisotropy）、區域型非等向性（Zonal Anisotroy）與混合型非等向性（Mixed Anisotropy）。
➢
幾何型非等向性變異 (Geometric Anisotropy)
幾何型非等向之變異圖，其Sill值僅依距離變化而改變，不因方向而變。換言之，在空間中的任何角度，當樣本點間的距離相同時，其Sill值亦相同，但影響範圍（range）則因角度之不同而異。影響範圍最大的方向為變異圖的方向，此範圍稱「主要影響範圍（Major Range）」。此時之變異圖稱為該角度之變異圖（Directional Variogram），影響範圍最小者稱為最小影響範圍。若將各角度之空間影響範圍繪於玫瑰圖上則呈現橢圓形。
|
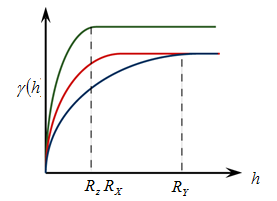
區域型非等向之變異圖，其Sill值不僅依距離變化而改變，且因方向而變。換言之，在空間中的任何角度，當距離相同時其Sill值將不會相同，且影響範圍異因角度不同而異。
區域型非等向之變異圖模式由兩個以上之非等向變異圖組成。一般的自然現象較少出現此種之非等向性。
|
➢ 混合型非等向性變異 (Mixed Anisotropy)
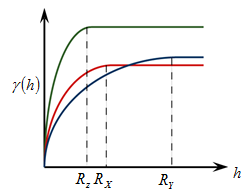
混合型非等向性變異為幾何與區域非等向性兩者之混合，其Sill值與影響範圍皆因方向不同而變。自然界常出現此一空間變異。例如地質之變化常於水平方向較垂直方向之影響範圍大，且垂直方向之變化較水平方向大。
|
©2017 Supergeo Technologies Inc. All rights reserved.