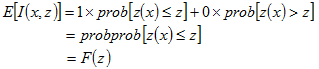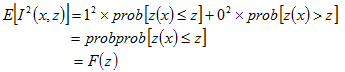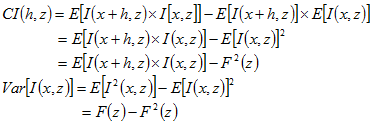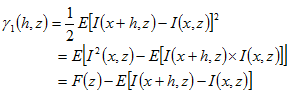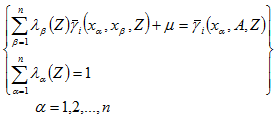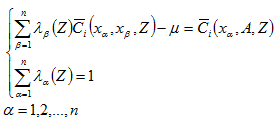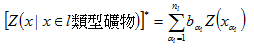指標克利金推估法
指標克利金是一種非參數的地理統計學,其不必去除重要而實際存在的高實際值數據,進行各項分析,並可求得在一定風險條件下,未知量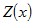 的估計量及空間分佈。
的估計量及空間分佈。
• 指標函數
指標函數
假設在空間範圍D中,於x位置取得樣本值隨機變數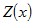 ,選定一臨界值Z,則在上的每一樣本點 ,選定一臨界值Z,則在上的每一樣本點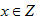 上定義Z的指標函數為: 上定義Z的指標函數為:

在上D的任一區域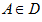 內,低於Z值的隨機變數 內,低於Z值的隨機變數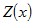 所佔區域A的比例表示為: 所佔區域A的比例表示為:
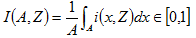
高於Z值的隨機變數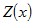 所佔區域A的比例表示為: 所佔區域A的比例表示為:
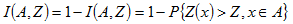
在臨界值Z的條件下,隨機函數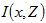 為二項式分配,其期望值為: 為二項式分配,其期望值為:
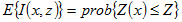
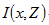 與 與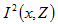 的期望值可表示成下式: 的期望值可表示成下式:
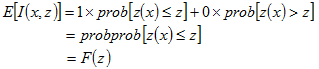
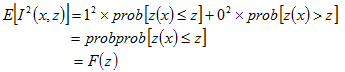
距離h,兩位置的指標函數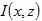 與 與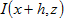 其共變數、變異數和半變異數分述如下: 其共變數、變異數和半變異數分述如下:
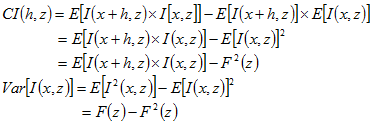
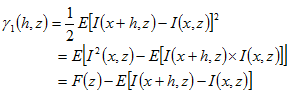
|
• 指標克利金方程組
指標克利金方程組
假設空間範圍D中,有N個有效樣本點,在D範圍內之一區域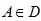 內有n個有效樣本點 內有n個有效樣本點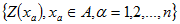 ,在設定臨界值之後,可得樣本的指標函數 ,在設定臨界值之後,可得樣本的指標函數 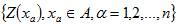 ,則 ,則 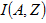 的估計值可以表示為: 的估計值可以表示為:
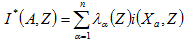
若給定一系列臨界值 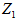 時 時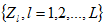 時,改寫為: 時,改寫為:
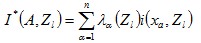
為求算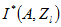 ,在滿足無偏與估計變異數最小化的條件下,計算權重係數 ,在滿足無偏與估計變異數最小化的條件下,計算權重係數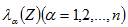 ,須解以下指標克利金方程組: ,須解以下指標克利金方程組:
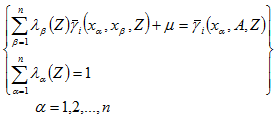
指標克利金的變異數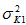 表示為: 表示為:
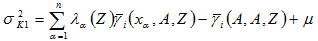
共變異函數可表示為:
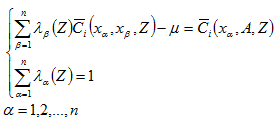
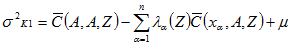
|
• 待估計區域A平均樣本的指標克利金估計
待估計區域A平均樣本的指標克利金估計
指標克利金法是應用某種克利金法求得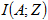 的線性估計值 的線性估計值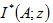 ,最後得到待估計區域A的平均樣本及儲量。在以下例子中,我們將待估計域設定在位置x上,分幾種情況討論如何使用指標克利金法求待估域的估計值 ,最後得到待估計區域A的平均樣本及儲量。在以下例子中,我們將待估計域設定在位置x上,分幾種情況討論如何使用指標克利金法求待估域的估計值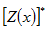 。 。
1. 例一: 例一:
由兩種礦物類型組成的礦床中位置x的平均樣本的估計。此時,指示值定義如下:

則,任一位置x上的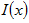 的平均值 的平均值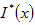 為: 為:


上述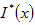 及 及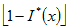 的值,均在0與1之間,即 的值,均在0與1之間,即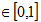 。位置x上1類型礦物的品位是根據x周圍 。位置x上1類型礦物的品位是根據x周圍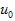 個1類型礦物品位值 個1類型礦物品位值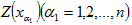 求得: 求得:

位置x上2類型礦物的品位是根據x周圍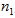 個2類型礦物品位值 個2類型礦物品位值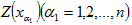 求得: 求得:

最後,位置x 的估計樣本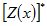 可由上面三式組合得到: 可由上面三式組合得到:
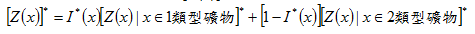
|
2. 例二: 例二:
由一種礦物類型(1>2)組成的礦床中位置x的平均樣本的估計實際工作中,任一位置x上只能有一種礦物類型佔優勢,此時:

位置x屬於第1型礦物的機率為:

同上可得:
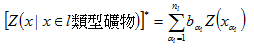
最後,位置x的估計樣本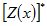 為: 為:
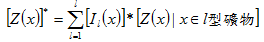
|
|
©2017 Supergeo Technologies Inc. All rights reserved.

![]() 的估計量及空間分佈。
的估計量及空間分佈。![]() 指標函數
指標函數![]() 指標克利金方程組
指標克利金方程組