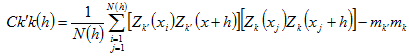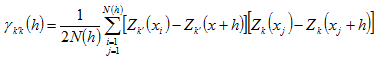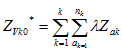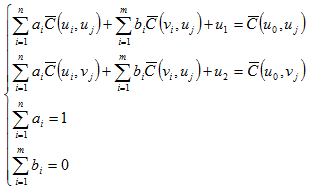研究聯合區域化現象與研究單一變數現象方法類似。假設K個聯合區域化變數，組成一組K維區域化變數的向量。在觀測前，它是一個K維區域化向量，觀測後則可視為K維空間向量。在二階定常性假設條件下，聯合區域化變量為：

1.每一個的數學期望平穩（Stable）存在，即。

2.每個區域化隨機變數，的共變異函數為：

上式中，K, ，當時，K,的順序不能任意顛倒。

當h=0時：

上式為與的變異數，或是普通統計學中兩個變數之間的共變異數。

3.滿足內在假設條件下，的增量的數學期望值為零，則每一為區域化變數與的共變異函數存在，且為：

與僅與h有關，與x無關。

在點x與點x+h處，分別測得兩個變量的觀測值 ，則共變數計算公式為：

上式中，，為樣本對數。

共變異圖的計算公式為：

聯合克利金法在理論上與普通克利金法本質相同，可以用推導普通克利金的過程推導聯合克利金。假設研究區域上有K個變數構成聯合區域化變數，滿足二階定常性與內在假設條件，即共變數與共變異圖存在。

估計中心點為x0，範圍為Vk0的平均值，即

在範圍Vk0附近有n個已知觀測樣本，其小區域範圍為vak，則Zak的平均值，為：

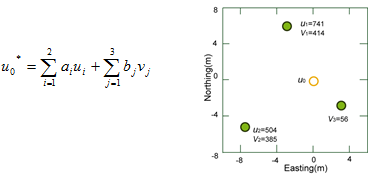
Zvk0的估計量為，是K個聯合區域化隨機變數全部有效觀測值的線性組合，聯合克利金線性估計量：

若在點x0處的某變數平均值為u0，在x0附近有兩筆觀測的聯合區域隨機變數和。則平均值u0的估計值構成的聯合克利金線性估計量為：

其中，為聯合克利金權重係數，為使為u0的最佳無偏線性估計，則需滿足無偏性與最佳化條件，經整理後，兩個變數的聯合克利金線性方程組之一般式為：

上述為n+m+2階線性方程組，解該線性方程組可得聯合克利金權重係數與，可得聯合克利金線性無偏最佳估計量，此時的聯合克利金估計變異數為：

假設研究區域內有兩個聯合區域化隨機變量u與V，其中為待估樣點，在周圍有已知樣點和的聯合克利金估計量。

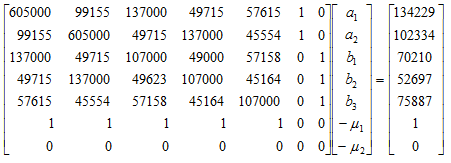
根據已知的理論模型計算量各變量的聯合共變異函數Cu（h）和Cv（h）及交叉共變異函數Cuv（h），則聯合克利金線性方程組為：

解上述方程組得：

將這些聯合克利金權重係數代入聯合克利金線性估計量方程中，可得的估計值：

其聯合克利金估計共變異數為：