
普通克利金推估法
當區域化變數Z(x)的數學期望值![]() ,m為未知常數時,採用普通克利金法。假設待估計區塊為V,中心為x,其平均值為Zv,則
,m為未知常數時,採用普通克利金法。假設待估計區塊為V,中心為x,其平均值為Zv,則
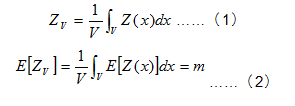
在待估計區塊V的區域範圍內,有一組已知n個樣點![]() ,其觀測值為Z(xi),其數學期望值也為m,即
,其觀測值為Z(xi),其數學期望值也為m,即![]() 。令
。令![]() 是Zv 的線性估計量,由n個已知的樣本觀測值Z(xi)構成的線性組合,即:
是Zv 的線性估計量,由n個已知的樣本觀測值Z(xi)構成的線性組合,即:
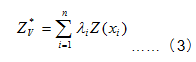
同樣在滿足無偏性與最佳化的條件下,![]() 成為Zv的線性、無偏、最佳化估計量。經整理後可得普通克利金估計變異數
成為Zv的線性、無偏、最佳化估計量。經整理後可得普通克利金估計變異數![]() ,即
,即
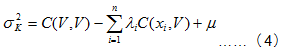
在變異函數存在條件下,也可用變異數函數表示普通克利金線性方程組與普通克利金估計變異數,即:
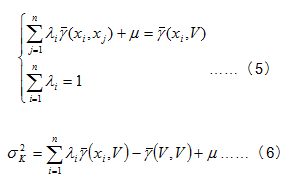
將解出的![]() 帶入公式(3)中得出普通克利金估計量
帶入公式(3)中得出普通克利金估計量![]() ,即
,即
![]()
待估計區塊V區域範圍內以xi為中心的區塊vi時,普通克利金線性方程組和普通克利金估計變異數為:
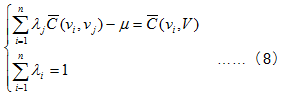
![]()
也可以用變異函數表示為:
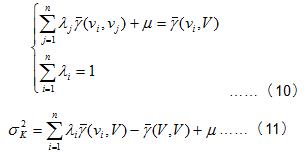
©2017 Supergeo Technologies Inc. All rights reserved.