Ordinary Kriging Estimation
When the mathematical expectation of the Kriging regionalized variable Z（x）is 
and m is an unknown constant, we use the Ordinary Kriging. Assuming that the region to be estimated is V, the center of it is x, its average is Zv, we can know
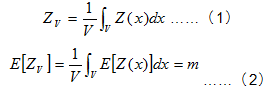
Where a dataset has n known sample points,
, in the range of estimation zone V, its observed value is Z(xi), and mathematical expectation is m. Therefore,
. Assuming that
is the linear estimator of Zv, the linear combination consisting of observed values Z(xi) of n known samples, we can obtain:
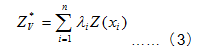
Under the same condition of satisfying the unbiased and optimization, is the best linear unbiased estimator of Zv. After calculation, we can obtain the Ordinary Kriging variance 
. It is:
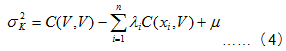
Under the condition of the existence of a variable function, we can also use a variablefunction to represent the Ordinary Kriging liner equations and Ordinary Kriging estimated variance:
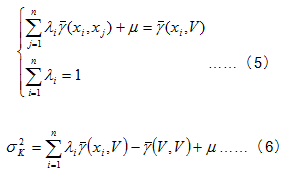
Where when we put the solution 
into the formula (3), we can obtain a Ordinary Kriging estimator 
, which is B:
When the zone vi with its center xi is within the extent of the estimation zone V, the Ordinary Kriging liner equations and Ordinary Kriging estimated variance are:
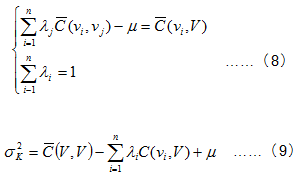
They are also could be presented by the variable functions:
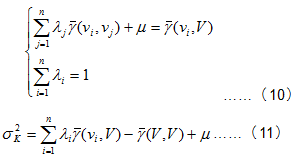
©2017 Supergeo Technologies Inc. All rights reserved.