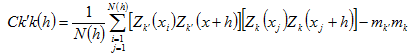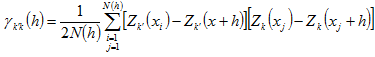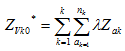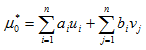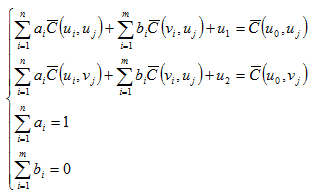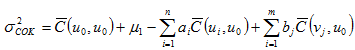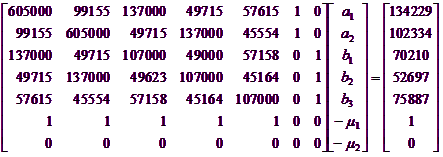Studying a joint regionalized phenomenon resembles studying a single variable phenomenon. Assuming that K joint regionalized variables,, consist of a pair of vectors of K dimension regionalized variables, before observation, they are K dimension regionalized vectors; after observation, they could be seen as K dimension spatial vectors. Under the condition of the hypothesis of second-order stationary, the joint regionalized variables are :

1.The mathematical Stable of each  exists, which is:

2.The cross covariance of each regionalized random variable is:

In the above equation, K,. When, the order of K, cannot be reversed. When h=0, the equation is:

The above equation is the variance of and, or the Cross Covariance between 2 variables in ordinary statistics.

3.When the inner assumed conditions are satisfied, the mathematical expectation of the increment of is 0, and the cross covariance of each regionalized variable and exists, which are:

and only have relations with h, but not x.

At point x and point x+h, we measure the observed values for the 2 variables, respectively. They are. The equation of the cross covariance is:

where ， is the sample pairs.

Equation for Cross Variogram is:

Theoretically, Co-Kriging has the same nature as the Ordinary Kriging. We can use the Ordinary Kriging derivation to derivate Co-Kriging. Assuming that there are k variables in a research area consisting of the joint regionalized variable, when the hypothesis of second-order stationary and intrinsic hypothesis conditions are satisfied, the cross covariance and cross variogram exist.

Where the estimated center is x0, and the range is the average of Vk0. We can obtain:

Where there are n known observed samples nearby range Vk0, and the range of its small region is vak. The average of Zak is:

Where the estimator of Zvk0 is. It is the linear combination of all the effective observed values of K joint regionalized random variables. The Co-Kriging linear estimator is:

If a variable average at point x0 is u0 and there are 2 joint regionalized random variables, and near x0, then the Co-Kriging linear estimator consisting of the estimateof the average u0 is:

Where and are the weight coefficients of Co-Kriging. In order to makebecome the best linear unbiased estimator of u0, we need to satisfy the conditions of unbias and optimization. After calculation, we can obtain the general form of the Co-Kriging linear equations of the 2 variables:

The above equation is n+m+ second-order linear equations. After solving the linear equations, we can obtain the weigh coefficients and and the best linear unbiased estimator of the Co-Kriging. At this time, the estimated variance of the Co-Kriging is:

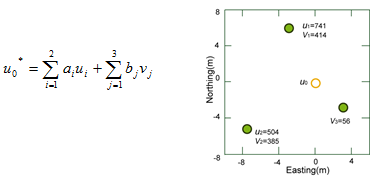
Assuming that there are 2 joint regionalized random variables u and V in a research area, where u0 is the sample point to be estimated. There are known sample points , and around u0. is the Co-Kriging estimator of u0.

According to the known theoretical models to calculate the joint covariance functions Cu（h）and Cv（h）and the cross covariance function Cuv（h）of each variable, the Co-Kriging linear equations are:

We can solve the above equations to obtain:

When we put the Co-Kriging weigh coefficients into the Co-Kriging linear estimation equations, we can obtain the estimator of

Where the Co-Kriging estimated Cross Covariance is: